Emma Bingham defended and received her PhD in Quantitative Biosciences on November 21st, 2025. Her thesis was titled “Biophysical Scaffolding in the Evolution of Complexity”, and she investigated how nascent multicellular organisms overcome the challenges of large size before the evolution of tissues specialized for transporting nutrients. Emma joined the Yunker Lab in 2021. Outside of lab, she enjoys reading, baking, and visiting farmers markets to find fresh vegetables.
Pablo defended and received his PhD in Quantitative BioSciences on May 21, 2024, with the title “Topographic Characterization of Biofilm Growth”. Pablo was originally from Chile. In the Yunker Lab, he was examining the surface-air interface of biofilms and what it can describe about their history and composition. He was mostly interested in bulk microbial community dynamics. In his free time, Pablo enjoyed grabbing a coffee and reading at a local coffee shop in Midtown, Atlanta or making a mean Barbeque. Pablo is currently working as a postdoc with Sujit Datta at Caltech.
Aawaz defended and received his PhD in Physics on June 17, 2024, with the title “Biophysical Basis of Bacterial Colony Growth,” where he investigated how bacterial biofilm shapes arise from underlying forces and impact the expansion of the biofilm on a given surface. Aawaz joined the Yunker Lab in the Spring of 2020. Currently, he works as a Senior Application Scientist at DigiM Solutions LLC in Boston. He enjoys deep philosophical conversations, playing music, and watching stand-up comedy.
We have a new paper on Physical Biology titled, “Biofilm vertical growth dynamics are captured by an active fluid framework”. It was first authored by Dr. Raymond Copeland.
In this study, we showed that biofilm vertical growth dynamics can be rigorously described using an active fluid framework. Our model demonstrated that death–decay and reaction diffusion dynamics are central determinants of biofilm height, unifying empirical heuristic models with biophysical theory. This work provides a predictive framework for microbial architecture and highlights new physical levers for controlling biofilm development.
We have a new paper on bioRxiv on how friction influences the development of bacterial biofilm. It was co-first-authored by Dr. Aawaz R. Pokhrel and Dr. Raymond Copeland.
In this work, we demonstrated that cell–substrate friction is a key physical parameter controlling biofilm morphology and expansion. Using white-light interferometry, we quantified how increasing surface friction increases biofilm contact angles and slows horizontal growth, consistent with a dynamic force balance model. These results establish friction as a general and overlooked determinant of biofilm development across diverse bacterial species.
Raymond Copeland defended and received his PhD in quantitative biosciences April 25th this year titled “Physical Simulations of Microbial Communities Under Stress” where he investigated how microbes grow, compete, and evolve resistance in complex communities using a combination of computational modeling, mathematics, and imaging. Ray joined the Yunker lab in early 2020 while he was still an undergraduate at Georgia Tech and stayed for graduate school to continue work with Dr Yunker and his friends. He enjoys classical music, chess, video games, and his wife Zoe. Ray remains at Georgia Tech to work as a postdoc with Dr Yunker
We have a new paper in Science Advances on how snowflake yeast overcome diffusion limits via metabolically-driven flow. It was co-first-authored by Emma Bingham, in collaboration with the Thutupalli lab at NCBS and the Ratcliff lab at Georgia Tech.
The ecological and evolutionary success of multicellular lineages stems substantially from their increased size relative to unicellular ancestors. However, large size poses biophysical challenges, especially regarding nutrient transport: These constraints are typically overcome through multicellular innovations. Here, we show that an emergent biophysical mechanism—spontaneous fluid flows arising from metabolically generated density gradients—can alleviate constraints on nutrient transport, enabling exponential growth in nascent multicellular clusters of yeast lacking any multicellular adaptations for nutrient transport or fluid flow. Beyond a threshold size, the metabolic activity of experimentally evolved snowflake yeast clusters drives large-scale fluid flows that transport nutrients throughout the cluster at speeds comparable to those generated by ciliary actuation in extant multicellular organisms. These flows support exponential growth at macroscopic sizes that theory predicts should be diffusion limited. This demonstrates how simple physical mechanisms can act as a “biophysical scaffold” to support the evolution of multicellularity by opening up phenotypic possibilities before genetically encoded innovations.
We have a new paper in Physical Review X on Morphological Entanglement in Living Systems, first-authored by Dr. Thomas Day and in collaboration with friends in the Ratcliff Lab at Georgia Tech.
Many organisms exhibit branching morphologies that twist around each other and become entangled. Entanglement occurs when different objects interlock with each other, creating complex and often irreversible configurations. This physical phenomenon is well studied in nonliving materials, such as granular matter, polymers, and wires, where it has been shown that entanglement is highly sensitive to the geometry of the component parts.
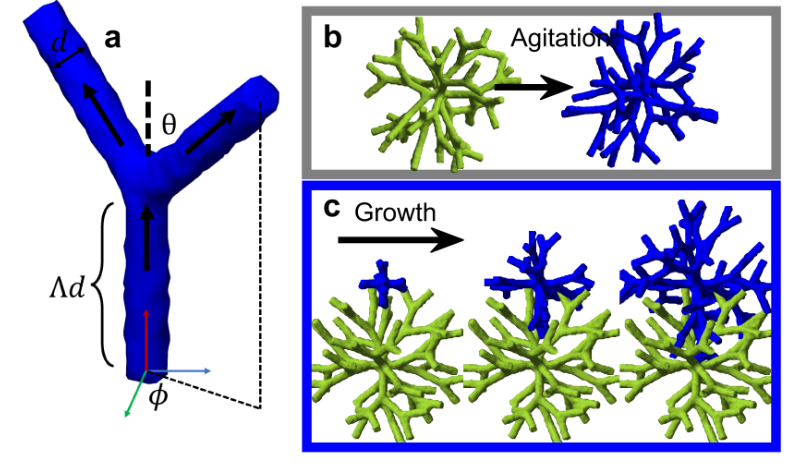
However, entanglement is not yet well understood in living systems, despite its presence in many organisms. In fact, recent work has shown that entanglement can evolve rapidly and play a crucial role in the evolution of tough, macroscopic multicellular groups. Here, through a combination of experiments, simulations, and numerical analyses, we show that growth generically facilitates entanglement for a broad range of geometries. We find that experimentally grown entangled branches can be difficult or even impossible to disassemble through translation and rotation of rigid components, suggesting that there are many configurations of branches that growth can access that agitation cannot. We use simulations to show that branching trees readily grow into entangled configurations. In contrast to nongrowing entangled materials, these trees entangle for a broad range of branch geometries. We, thus, propose that entanglement via growth is largely insensitive to the geometry of branched trees but, instead, depends sensitively on timescales, ultimately achieving an entangled state once sufficient growth has occurred. We test this hypothesis in experiments with snowflake yeast, a model system of undifferentiated, branched multicellularity, showing that lengthening the time of growth leads to entanglement and that entanglement via growth can occur for a wide range of geometries. Taken together, our work demonstrates that entanglement is more readily achieved in living systems than in their nonliving counterparts, providing a widely accessible and powerful mechanism for the evolution of novel biological material properties.
The most recently graduated member of the Yunker Lab, Thomas studied how physics constrains the evolution of early multicellular organisms. He defended his thesis in February 2023. It was titled Biophysical Constraints of Multicellularity: Building a Darwinian Material.
“Speedy” Tom Day grew up in the small town of Haddam, Connecticut, and ran Cross Country and Track & Field at Lafayette College while pursuing his undergraduate degree. At Georgia Tech, he kindled a new love for long bike rides. Among other activities, he also enjoys playing and listening to live music; this has led to an emergence of an N+1 problem, regarding how many instruments he owns vs. how many he needs.
Tom left Georgia Tech to start a postdoc with Julia Schwartzman at USC. He was a core part of our lab’s social and scientific lives, and we will miss him greatly. We are excited to see what Tom will do in the future!
We have a new paper out on the evolution of macroscopic multicellularity.
See also this article on our paper from the New York Times.